Геометрическое моделирование

Платоновы тела

Куб	Додекаэдр	Икосаэдр	Октаэдр	Тетраэдр

Можно придумать разные способы для сборки многогранников. Наверное, самый простой - делать их из соломы. Последовательность сборки соломенного октаэдра - на рисунке.

Чтобы связать октаэдр, сначала нарезают 12 соломин одинаковой длины и толщины. Затем их нанизывают на нить с помощью толстой иглы. Четыре крайние соломины связывают в квадрат, у одной из сторон которого размещают две соломины так, чтобы получился треугольник. Такие треугольники выполняют на каждой стороне квадрата. Первую пару соломин треугольника перекручивают через основание к центру квадрата, вторую пару - от центра, третью - к центру, четвертую - от центра. Когда будет перекручена четвертая пара, оставшийся конец нитки связывают с другим концом. В результате должна получиться плоская фигура с квадратом в центре. Чтобы получить пространственную ромбическую фигуру, нужно поднять вверх второй и четвертый треугольники и связать их вместе, а первый и третий - отвести в противоположную сторону и тоже связать. Для того чтобы соломенные трубочки не разрезались нитью, их следует увлажнить перед сборкой ромбов. Для обеспечения жесткости конструкции в целом можно в основной несущий ромб вдеть гибкую проволоку, углы же остальных ромбов зафиксировать клеем ПВА.

По материалам ежедневной всеукраинской газеты "День"

Это действительно самый простой способ. Но есть и другие.

Правильные многогранники, да и вообще, любые геометрические формы можно собирать из дерева. Необходимый для этого деревянный брусок сечением 6х6 мм., 1х1см. можно приобрести на базаре, где он продается под видом самого простого оконного штапика. Далее остаётся взять лобзик и вырезать планочки нужной длины. А чтоб можно было их склеить, каждую необходимо обрезать по шаблону, приводимому ниже. Для каждого многогранника - свой шаблон.

Сделанные по этим шаблонам многогранники при надлежащей аккуратности
жёстко сохраняют свою форму и могут использоваться как гармонизаторы пространства
- для приведения в порядок мыслей, очищения ума, создания настроения.

Вот так будут выглядеть срезы планочек под склейку
для каждого из вышеперечисленнных многограников последовательно.
Скачать все схемы одним архивом

Впрочем, если Вы больше доверяете линейке и карандашу, расчертить шаблоны можно самостоятельно в соответствии со следующей таблицей:

	тетраэдр	куб	октаэдр	икосаэдр	додекаэдр
a	17.071	10	17.071	15.811	7.071
b	20	10	14.042	8.74	5.402

*таблица рассчитана под сечение планочки 10х10

Это фигура, получающаяся из октаэдра при делении каждой его грани тремя ребрами
и элемент (модуль), из которых она собирается. 24 модуля - и модель готова.

Прорезные бумажные модели

Ещё один способ изготовления геометрических форм - из бумаги. Чтобы сделать бумажный шар-многогранник,  нужна плотная бумага, циркуль и ножницы.

Из круга с пятью прорезями получается додекаэдр, с тремя - октаэдр или тетраэдр.

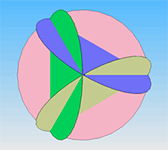
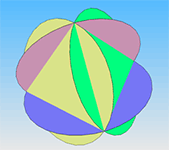
Проявив немного изобретательности, можно собрать и другие модели:

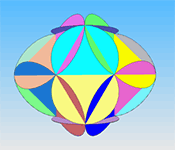
Все это разные проекции одной модели. Это четырехлепестковые пирамиды, собранные основаниями  в каркас куба. Если пойти еще дальше, то прорези можно делать нелинейными. Следующие две модели именно такого класа. Их грани вогнутые.

Восьмилепестковая бипирамида

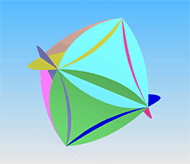
Шестилепестковая бипирамида

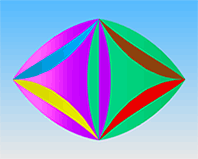
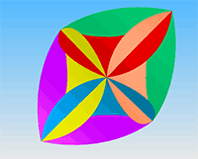
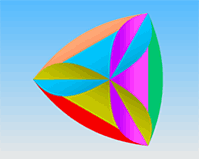
Для четырёхугольной и треугольной вогнутых бипирамид приведены выкройки. Соотношение всех размеров приближено к идеальному, но радиус внутренней вогнутости приблизителен (строго говоря, это не радиус, а некая кривая). Поэтому для точного совпадения и стыковки всех единиц можно скопировать контуры с рисунка.

Все прорези должны делаться в одном направлении. Внешние радиусы не обязательно строго выдерживать, они лишь подчеркивают объём, придают образ шара всей конструкции.

Эти бумажные модели, если их правильно сделать, и подобрать подходящие для человека цвета, очень интересны. Кажется, что это душа человека.
Такая же лёгкая, почти невесомая.

Обычно для передачи настроения достаточно трёх – четырёх пар лепестков разного цвета. А ещё иногда спрашивают: “А как Вы догадались, что это мой любимый цвет?”

Уравновешенным и спокойным, мягким, впрочем, большинству я дарю вариант четырёхугольной пирамиды.

Людям креативным и творческим, напористым - вариант треугольной пирамиды.

Самое удивительное, что первоначальный вариант, сделанный на глазок, без промеров и моделирования, не стыкующийся в точках вершин по определению, мне нравится даже больше.

Галерея придуманных моделей достаточно велика. Каждая форма несёт своё настроение. Спроектировать модель можно для каждого человека индивидуально.
Правильные многогранники – платоновы тела в этом смысле универсальны. Это основа.

Это уже не просто модель, а прибор. Универсальный модуль. Его используют в техниках медитации. Подробнее узнать об этом можно на сайте http://aiskhen.ru Впрочем, любая качественно сделанная модель может служить объектом созерцания и приносить с собой ясность мыслей и ощущение праздника.

На этой странице практически ничего не сказано о модульном оригами. Кое-что можно найти в книге "Введение в формологию". А еще проще - на сатах, посвященных этой тематике.